使用扫描式测头之五轴工具机双旋转轴几何误差同步量测系统

文◆国立成功大学 机械工程系 阎庆贤、指导教授 刘建圣

一、研究目的

现代制造技术的发展，高精度与高效率的加工需求增长，五轴工具机在航空航天、汽车制造等领域应用广泛。然而高精度加工也带来了复杂的误差控制挑战，直接影响成品质量及机台寿命，故五轴工具机的误差量测成为重要研究课题。其中几何误差源于机床制造与组装中的非理想几何偏差，如轴向、角度、直线度等误差，对加工质量影响显著且会累积，故其量测与补偿至关重要。

现商用仪器主要存在两大问题：一是单次测量通常只针对少数几何误差项，忽略了其他误差源的耦合效应及多轴同时运动时的误差迭加。二是现有仪器多仅量测安装误差或单运动轴的误差，忽视不同位置下运动误差的影响。前人的研究已探讨单轴运动旋转轴误差与双轴运动下的安装误差，但鲜少兼顾两者。故本文旨在开发针对五轴工具机的高精度几何误差量测技术，提出能同时解析双旋转轴共20项几何误差的系统，并考虑误差耦合及动态影响。

二、研究方法

1.实验设备、载具

本文使用的实验载具为小型立式五轴加工机，图1展示了其外观。该机床具备全工作台旋转型设计，拥有五轴同步加工能力，其A轴与C轴的旋转功能增加了工件定位的自由度，使工具几乎能从任意角度接近工件，适合加工航空零件、汽车复杂组件及高精度模具等复杂外形部件。

本文使用的量测设备为工具机上的测头系统，该系统在高精度制造中扮演关键角色，确保加工精度、提升生产效率并优化制程。测头系统透过精确测量工件与刀具位置，支持五轴加工机的高性能运作。

常见的触发式测头透过接触工件表面触发讯号，提供高精度的位置信息，其可分为单点接触式与扫描式测头，单点接触式测头适用于点位量测，常用于简单且精确的测量任务；扫描式测头则能在工件表面连续移动，收集大量数据点，提供更详细的表面轮廓信息，适合复杂曲面和精细特征的测量。

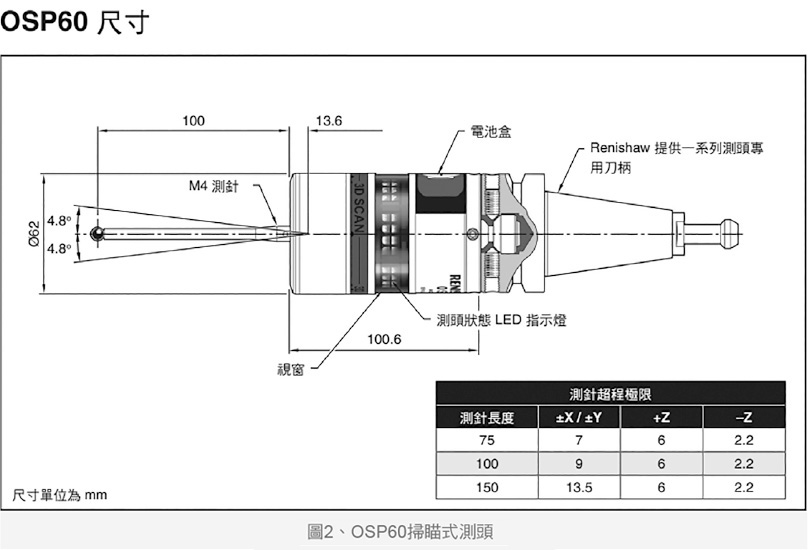
本文使用OSP60扫描式测头系统（如图2），与单点触发测头相比能快速沿着工件表面移动，收集大量数据点与方向信息，特别适用大面积或多点测量的情况，有助于更精确地捕捉工件表面的轮廓及复杂几何形状，对于精度的质量控制尤为重要且缩短了测量时间，提高了细节分析与检测能力。

2.量测系统、方法

本文开发之量测系统使用OSP60扫描式测头进行量测，量测一良好的平面度之方块与一高精度校正球。避免由球体半径误差带来的量测不确定性及方块表面平面度之影响。量测过程中，校正球磁吸于摇篮上，方块则锁固于转台，测头安装于主轴，具体安装情况如图3所示。测头系统抓取校正球心及方块固定点作为初始位置，随后转动双旋转轴并量测旋转后的球心位置及方块表面轮廓信息。所有量测过程由NC code设计之自动程序完成，并将所得数据代入本文提出的数学模型中计算误差。量测过程中需注意减少不确定性误差来源，并确保所有设备经市售量测仪器补偿及温度控制，以得到最精确的结果。

量测原理分为校正球与方块两部分。图4显示方块安装于C轴转台上，由于工具机零件在安装时的不精确产生安装误差，C轴与A轴产生径向偏移与偏摆，双轴的误差耦合影响方块运动，使其移至Position1，并产生体积误差dP (PIGE)。接着考虑运动误差影响。

运动误差来自于工具机零件制造时的瑕疵，导致零件之间的相对运动产生偏移与偏摆，使方块产生另一体积误差dP(PDGE)，并移动到Position2，Position2与ideal position即实际位置与理想位置之间的偏差，也就是总体积误差dP。透过建立体积误差与旋转轴几何误差的关系，可以解析双旋转轴的安装与运动误差。系统透过拟合方块尖点位置，量测方块平面的法向量和一点位置，求出平面方程式，再联立三个平面方程式计算尖点的机械坐标值，避免测量误差。接着考虑平面法向量的偏摆与旋转轴几何误差之间的关系。

图4显示方块尖点受几何误差影响产生体积误差，使平面法向量出现方向上的体积偏摆dV，同理分为安装误差影响的dV(PIGE)和运动误差影响的dV(PDGE)，其中仅偏摆误差会影响法向量的方向。透过建立旋转轴偏摆几何误差与法向量之间的关系，量测方块上各平面法向量的偏差值即可求出体积误差信息以解析旋转轴几何误差。

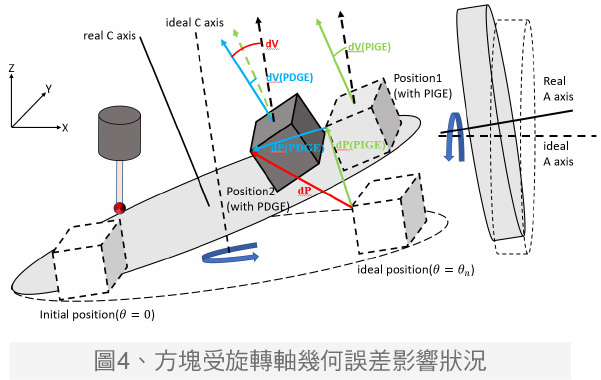
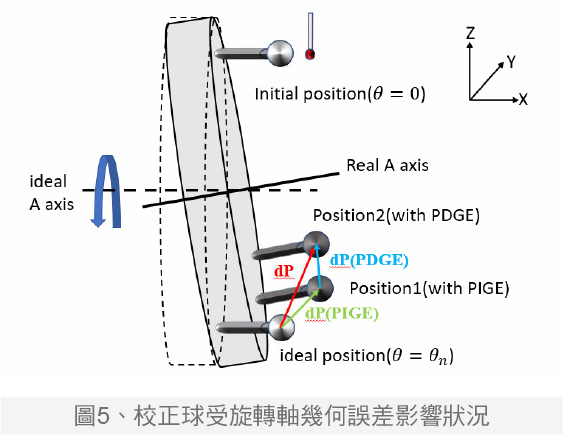
图5显示了校正球在几何误差影响下产生的偏差。本文的量测系统将校正球置于A轴摇篮机构上，因此当旋转轴转动时，球心位置只受A轴安装误差移动到Position1，再受运动误差的影响移动到Position2，并产生体积误差。这样的设计可分离A轴几何误差的影响，同时解析转台上方块尖点的体积误差，便于设计量测路径。

本文量测实验具体流程如下，将扫描式测头安装于主轴，校正球置于A轴，方块置于C轴。排除测头误差并在A、C轴角度为0的初始位置测量校正球与方块的坐标，执行自动量测程序进行各角度测量，记录几何信息并计算误差项。

测头测量程序由NC code程序开发，通过圆路径扫描、线路径扫描及单点触发进行自动测量，拟合出不同角度下校正球圆心坐标与偏差(XYZ center error)、线路径初始点法向量方向坐标偏差(Start point error)与路径角度偏差(Best fit angle)。

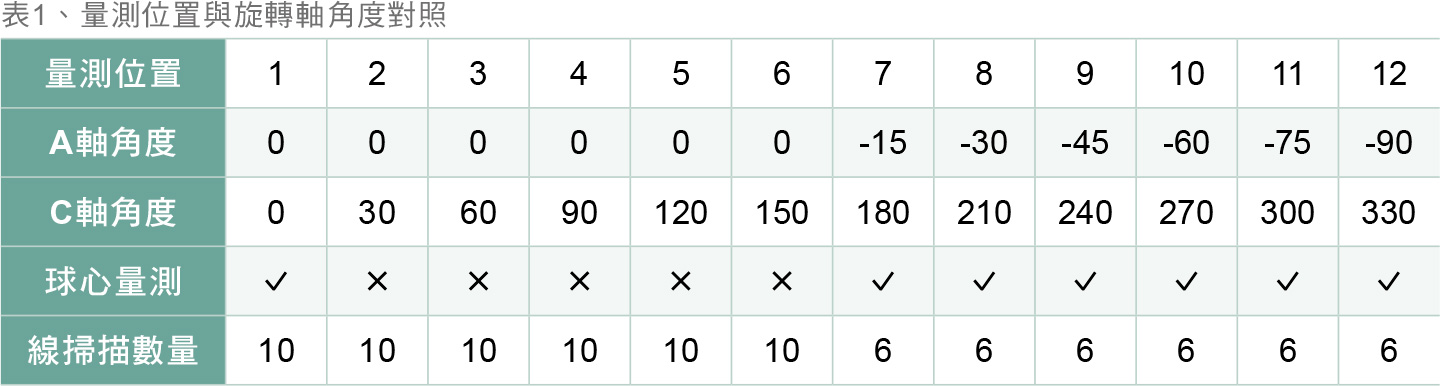
表1总结了12组旋转轴位置与量测的关系。扣除初始位置，实验共解析110个误差项，包括A轴的安装误差(4项)与运动误差(6自由度*6位置)及C轴的安装误差(4项)与运动误差(6自由度*11位置)。A轴于初始位置和第7至12位置进行校正球量测XYZ center error，后六位置使用转换后校正球坐标进行测量。方块五个平面各自生成两条垂直路径，通过路径向量外积求得法向量，量测各平面的Start point error与Best fit angle，透过上述信息可以换算成体积误差偏移与偏摆，用以解析几何误差，部分旋转角度下由于姿态干涉问题略过某些平面测量。

3.運動學

了解析几何误差，本文建立了测头待测物的运动链关系，分别为：测头P → Z轴 → Y轴 → X轴 → A轴 → C轴 → 方块B，测头P → Z轴 → Y轴 → X轴 → A轴 → 基准球S两条运动链。由数学模型与齐次坐标转换矩阵以求得方块与校正球相对测头的关系。

在机械坐标与各运动轴、待测物建立多个坐标系，如工具机坐标系、测头坐标系、校正球坐标系等，并考虑各坐标系间的距离参数，如各轴间距离和旋转轴中心相对参考原点的距离，接着省略不影响结果之参数以优化后续运算，避免算式之冗长与无用之参数相乘项，图6(a)与图6(b)分别显示了运动链简化前与简化后的结果。

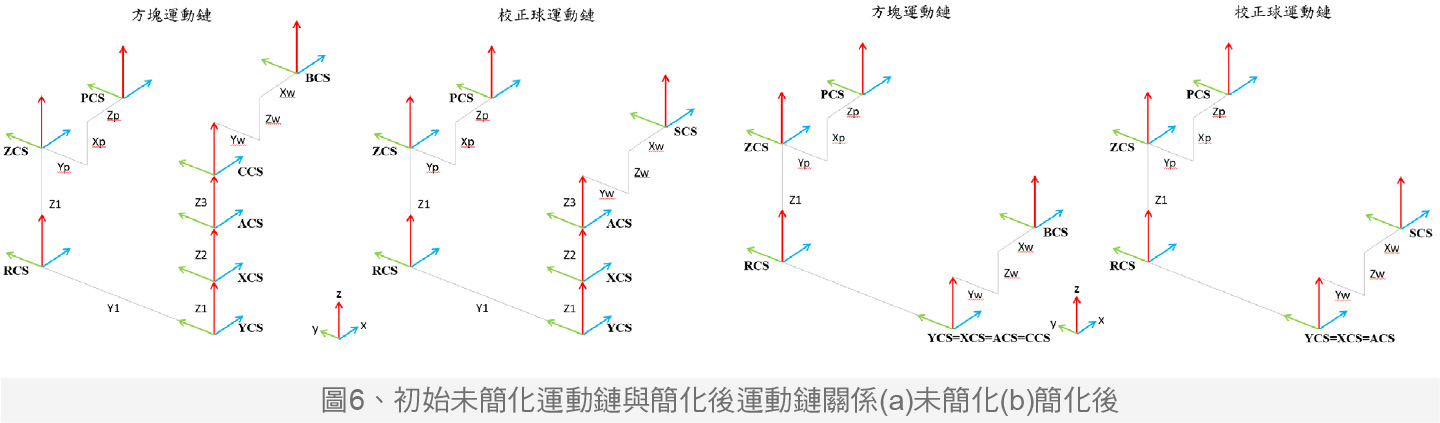
数学模型之推导方面，各坐标系以齐次坐标转换矩阵表示其运动情形，接着根据相对几何关系做矩阵的相乘，可得出各运动链对于机械原点之几何关系，并分为理想与实际包含误差之情形做运算，其结果包含了测头尖点(probe center position)、校正球之球心坐标(sphere center point)、方块尖点之机械坐标(block sharp point)、方块平面之法向量(plane normal vector)等信息。当测头的探针尖点碰触待测物时的位置是相同的条件可以视 测头尖点与校正球球心重迭、或测头尖点与方块尖点重迭，并分为理想与实际情况下解出各运动轴之驱动值x_cmd^i、y_cmd^i、z_cmd^i与x_cmd^r、y_cmd^i、z_cmd^i， 理想与实际驱动相扣便可得出几何信息与旋转轴几何误差之间的关系方程式，其中方程式变量包含量测角度θ_C和θ_A、方块B和校正球S相对于旋转轴坐标系的坐标值x_w、y_w、z_w，并通过最小化残差平方和来找到最佳的未知数解。在非线性情况下，可以使用迭代方法来近似求解，并将系统线性化来简化求解过程。依照本实验设计的量测路径，计算不同旋转轴角度位置下可获得的方程式数量，一次量测可获得180条方程式。将所有方程式的关系统整后得到A轴和C轴几何误差方程组并用以同时求解双旋转轴之几何误差。

三、实验结果

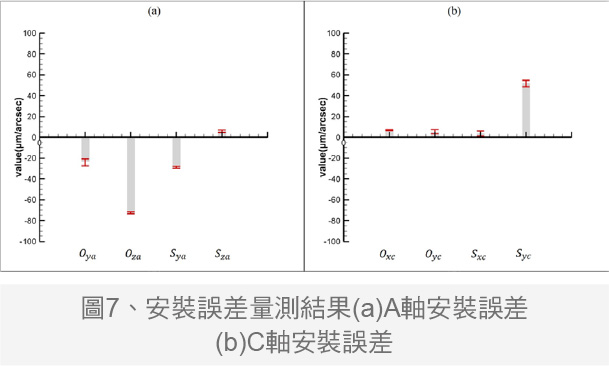
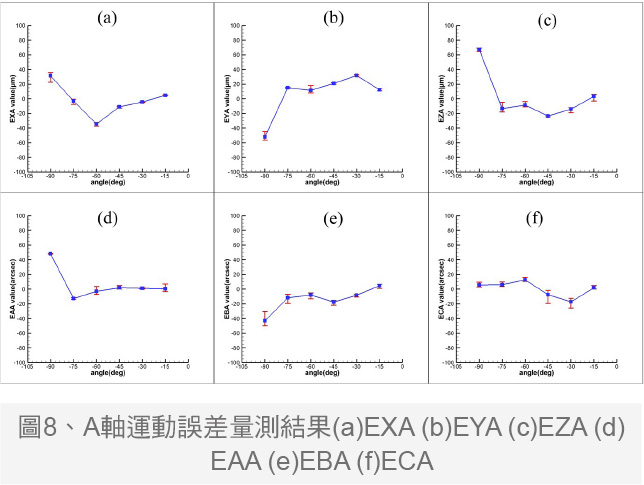
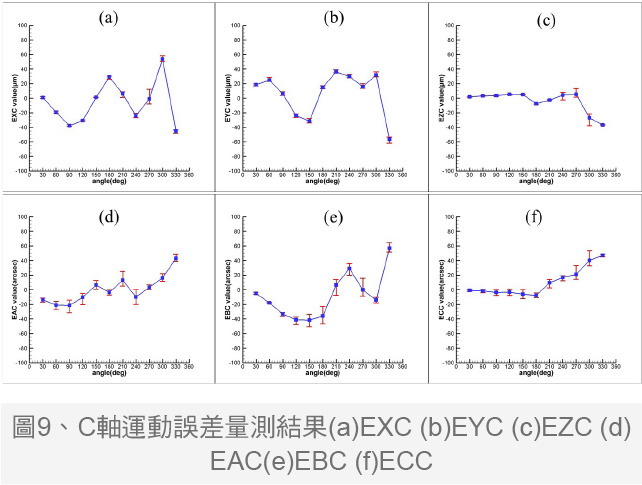
本文实际量测实验取五组结果取平均并比对各组结果之间的重复性表现，量测结果如图7至图9所示，由图7的量测结果分析，A轴的安装误差分别为-23.1704μm、-72.8639μm、-29.0082arcsec、5.8683arcsec；C轴的安装误差分别为7.0554μm、5.0641μm、3.6991arcsec、51.7812arcsec。A轴的偏移误差和C轴的偏摆误差较大，推测可能是其他零件的安装误差耦合造成，如线性轴的垂直度误差。系统解析时假设线性轴无误差，但实际上工具机存在线性轴误差，影响旋转轴的安装误差数值。

由于实验机台无补偿功能，且国内相关研究有限，本文采用数值比对法验证量测误差。现今机台制造厂商常用校正球定位法粗略估计旋转轴偏差，具体作法是在初始位置定位球心坐标，旋转轴至180°再定位第二组坐标，取两者平均得出旋转中心坐标偏移值。若增加至每90°一组坐标，通过拟合圆法可估算旋转轴安装误差与偏摆。此法虽不能精确量测安装误差，但能大致推算旋转中心与转动情形。

本文针对A轴，因行程限制无法涵盖完整圆路径，改以30°区间抓取四个坐标拟合最佳旋转中心。随后与前代学长发展的双旋转轴安装误差量测系统结果比对，显示误差分析结果基本相符。尽管各方法间有细微差距，可能由温度或振动等不确定因素造成，但差异在可接受范围内。前代学长发展的方法经过补偿验证具可靠性，拟合圆计算作为误差评估方法也具一定准确性，因此本文验证了误差计算结果的正确性。

四、结论与未来

本文针对五轴工具机提出一套量测系统，可同时量测双旋转轴的20项几何误差。该系统采用扫描式测头，具备动态量测功能，简单校正后即可快速自动执行量测。此方法不仅能解析更多几何误差，还具备价格低、安装操作便捷、测量时间短等优点。扫描式测头技术是一项创新，能够在移动中持续收集数据，相比传统单点触发式测头，可更快地获取工件表面的密集坐标点，适合五轴加工机进行复杂工件的全面量测。此外，该系统灵活应对不同构型的五轴机台，只需修改数学模型与程序，即可解析各构型的几何误差，提供精确解决方案。

未来发展方向包括系统智能化、自动化及多功能测量。透过人工智能技术，测头可实现自动校准与误差补偿，减少人工干预，提升测量精度与效率。亦可进一步扩展量测参数，如工件尺寸、形状、表面粗糙度等，实现全面质量检测。此外，亦可配合实时温度补偿技术可根据温度传感器数据自动修正测量结果，或利用热膨胀系数模型进行调整。同时，主动振动控制技术将通过反向振动进行抑制，并结合振动补偿算法修正测量结果，减少误差影响。